Deep Learning Theory : Quadratic models and nearly-kernel methods
Author: Hyunin Lee
Date: 12.24.2023
Day2
Lecture 2 is covers Chapter 11.4, chapter7.2 and chapter ∞.2.2 if this book[https://deeplearningtheory.com/lectures/]
0.Notations of Deep Neural Network
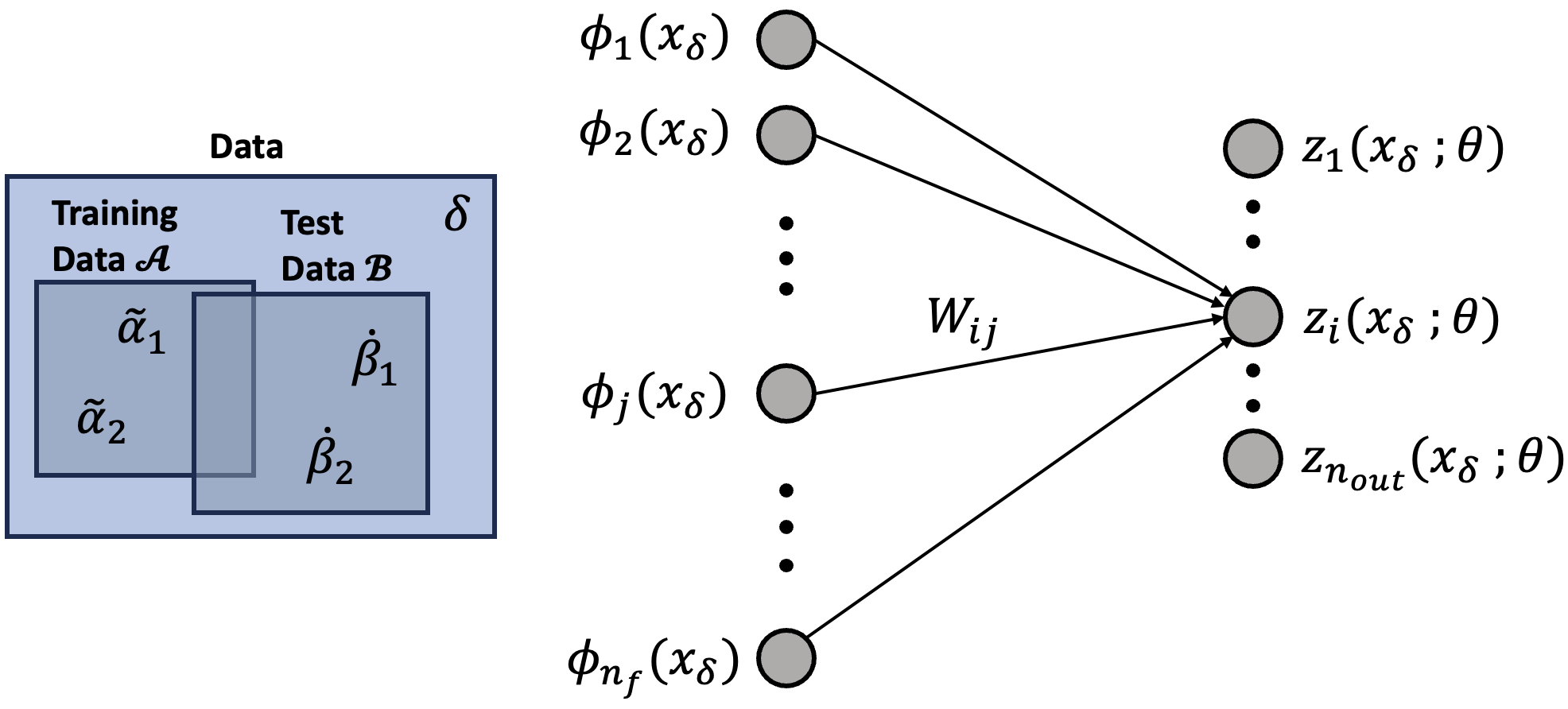
0.1 Definitions & Notations
- Feature function, Meta feature function
\(\phi_j(x_\delta), \psi_{j_1,j_2}(x_\delta)\)
- Effective feature function
\(\phi^E_{ij}(x_\delta; \theta) = \phi_j(x_\delta) + \varepsilon \sum_{k=0}^{n_f} W_{ik} \psi_{kj}(x_\delta)\)
- Residual training error
\(\epsilon_{i;\tilde{\alpha}} = z_{i;\tilde{\alpha}} - y_{i;\tilde{\alpha}}\)
- Effective kernel
\(k^{E}_{ij;\delta_1\delta_2} (\theta) = \sum_{j=0}^{n_f} \phi^{E}_{ij}(x_{\delta_1}; \theta) \phi^{E}_{ij}(x_{\delta_2}; \theta)\)
1. Linear Models and Kernel Methods
Two forms of a solution for a linear model:
- parameter space - linear regression
\[z_i(x_{\dot{\beta}}; \theta^*) = \sum_{j=0}^{n_f} W_{ij}^* \phi_j(x_{\dot{\beta}})\]
- sample space - kernel methods
\[z_i(x_{\dot{\beta}}; \theta^*) = \sum_{\tilde{\alpha}_1, \tilde{\alpha}_2 \in A} k_{\dot{\beta} \tilde{\alpha}_1} \tilde{k}^{\tilde{\alpha}_1 \tilde{\alpha}_2} y_{i;\tilde{\alpha}_2}\]
2. Nonlinear models
Let’s relax the above linear model into a nonlinear model, specifically a \textcolor{blue}{quadratic model}.
\[z_{i;\delta}(\theta) = \sum_{j=0}^{n_f} W_{ij} \phi_j(x_\delta) + \textcolor{blue}{\frac{\epsilon}{2} \sum_{j_1, j_2 = 0}^{n_f} W_{i j_1} W_{i j_2} \psi_{j_1 j_2}(x_\delta)}\]
- It’s nonlinear because it’s quadratic in the weights: ( W_{ij_1} W_{ij_2} ).
- ( \varepsilon ) is a small parameter that controls the size of the deformation.
- We’ve introduced ( \frac{(n_f + 1)(n_f + 2)}{2} ) meta feature functions, ( \psi_{j_1 j_2} (x) ), with two feature indices.
3. Quadratic models
To familiarize ourselves with this model, let’s make a small change in the model parameters $ W_{ij} \to W_{ij} + dW_{ij} $:
\[z_i(x_\delta; \theta + d\theta) = z_i(x_\delta; \theta) + \sum_{j=0}^{n_f} dW_{ij} \left( \phi_j(x_\delta) + \epsilon \sum_{j_1=0}^{n_f} W_{ij_1} \psi_{j_1 j}(x_\delta) \right) + \frac{\epsilon}{2} \sum_{j_1, j_2=0}^{n_f} dW_{ij_1} dW_{ij_2} \psi_{j_1 j_2}(x_\delta)\]
Let us make a shorthand for the quantity in the square bracket,
\[\textcolor{blue}{\phi^E_{ij}(x_\delta; \theta)} = \frac{dz_i(x_\delta; \theta)}{dW_{ij}} = \phi_j(x_\delta) + \varepsilon \sum_{k=0}^{n_f} W_{ik} \psi_{kj}(x_\delta),\]
which is a blue{effective feature function}.
4. Effective Feature Functions
The utility of this is as follows:
- The linear response of ( z_i(x_\delta; \theta) ) behaves effectively as if it has a parameter-dependent feature function, ( \phi^E_{ij}(x_\delta; \theta) ).
- The change in the ( \phi^E_{ij}(x_\delta; \theta) ) given ( W_{ik} \to W_{ik} + dW_{ik} ) is
\[\phi^E_{ij}(x_\delta; \theta + d\theta) = \phi^E\]
5. Quadratic Regression
Supervised learning a quadratic model doesn’t have a particular name, but if it did, we’d all probably agree that its name should be quadratic regression:
\[L_A(\theta) = \frac{1}{2} \sum_{\tilde{\alpha} \in A} \sum_{i=1}^{n_{out}} \left[ y_{i;\tilde{\alpha}} - \sum_{j=0}^{n_f} W_{ij} \phi_j(x_{\tilde{\alpha}}) - \frac{\epsilon}{2} \sum_{j_1, j_2 = 0}^{n_f} W_{ij_1} W_{ij_2} \psi_{j_1 j_2}(\tilde{x}_{\alpha}) \right]^2.\]
The loss is now quartic in the parameters, but we can optimize with gradient descent:
\[W_{ij}(t + 1) = W_{ij}(t) - \eta \frac{\partial L_A}{\partial W_{ij}} |_{W_{ij}=W_{ij}(t)}.\]
This will find a minimum in practice.
6. The Theoretical Minimum (linear model)
Let’s start by seeing how gradient descent solves the linear model:
\[L_A(W) = \frac{1}{2} \sum_{\tilde{\alpha} \in A} \sum_{i=1}^{n_{out}} \left[y_{i;\tilde{\alpha}} - \sum_{j=0}^{n_f} W_{ij} \phi_j(x_{\tilde{\alpha}}) \right]^2,\]
Then, we have
\[\begin{align*}
\frac{\partial L_A(W)}{\partial W_{ab}} &= - \sum_{\tilde{\alpha}, i, j} \delta_{ia}\delta_{jb} \phi_j(x_{\tilde{\alpha}}) \left[ y_{i;\tilde{\alpha}} - \sum_{j=0}^{n_f} W_{ij} \phi_j(x_{\tilde{\alpha}}) \right] \\
&= \sum_{\tilde{\alpha}} \phi_b(\tilde{x}_{\alpha}) (z_{a;\tilde{\alpha}} - y_{a;\tilde{\alpha}}) \\
&= \sum_{\tilde{\alpha}} \phi_b(\tilde{x}_{\alpha}) \epsilon_{a;\tilde{\alpha}}
\end{align*}\]
In the last line, we defined the residual training error:
\[\textcolor{blue}{\epsilon_{i;\tilde{\alpha}}} = z_{i;\tilde{\alpha}} - y_{i;\tilde{\alpha}}.\]
The weights will update as
\[\begin{aligned}
W_{ij}(t + 1) &= W_{ij}(t) - \eta \frac{d L }{dW_{ij}} \Big|_{W_{ij}=W_{ij}(t)} \\
&= W_{ij}(t) - \eta \sum_{\tilde{\alpha}} \phi_j(x_{\tilde{\alpha}}) \epsilon_{i;\tilde{\alpha}}(t)
\end{aligned}\]
For the theoretical analysis, it’s more convenient to understand how the output of the model updates:
\[\begin{aligned}
z_{i;\delta}(t + 1) &= z_{i;\delta}(t) + \sum_{a,b} \frac{\partial z_{i;\delta}(t)}{\partial W_{ab}} \left[ W_{ab}(t + 1) - W_{ab}(t) \right] \\
&= z_{i;\delta}(t) + \sum_{a,b} \frac{\partial z_{i;\delta}(t)}{\partial W_{ab}} \left[ - \eta \sum_{\tilde{\alpha}} \phi_b(x_{\tilde{\alpha}}) \epsilon_{a;\tilde{\alpha}}(t) \right] \\
&= z_{i;\delta}(t) + \sum_{a,b} \delta_{i a}\phi_b (x_\delta) \left[ - \eta \sum_{\tilde{\alpha}} \phi_b(x_{\tilde{\alpha}}) \epsilon_{a;\tilde{\alpha}}(t) \right] \\
&= z_{i;\delta}(t) - \eta \sum_{\tilde{\alpha}} \left[ \sum_{b} \phi_b (x_\delta) \phi_b(x_{\tilde{\alpha}}) \right]\epsilon_{i;\tilde{\alpha}}(t) \\
&= z_{i;\delta}(t) - \eta \sum_{\tilde{\alpha}} k_{\delta \tilde{\alpha}} \epsilon_{i;\tilde{\alpha}}(t)
\end{aligned}\]
- Fixed $k_{\delta \tilde{\alpha}}$ generates the dynamics of the model.
- $\epsilon_{i;\tilde{\alpha}}(t)$ sources the updates for general inputs $\delta \in \mathcal{D}$.
We have to solve a linear difference equation:
\[z_{i;\delta}(t + 1) = z_{i;\delta}(t) - \eta \sum_{\tilde{\alpha}} k_{\delta \tilde{\alpha}} \epsilon_{i;\tilde{\alpha}}(t).\]
Restricting to the training set, we get a first-order homogeneous linear difference equation,
\[z_{i;\tilde{\alpha}_1}(t + 1) = z_{i;\tilde{\alpha}_1}(t) - \eta \sum_{\tilde{\alpha}_2} \kappa_{\tilde{\alpha}_1\tilde{\alpha}_2} \epsilon_{i;\tilde{\alpha}_2}(t),\]
for the residual training error:
\[\epsilon_{i;\tilde{\alpha}_1}(t + 1) = \epsilon_{i;\tilde{\alpha}_1}(t) - \eta \sum_{\tilde{\alpha}_2} \kappa_{\tilde{\alpha}_1\tilde{\alpha}_2} \epsilon_{i;\tilde{\alpha}_2}(t),\]
We can rewrite these dynamics:
\[\epsilon_{i;\tilde{\alpha}_1} (t + 1) = \sum_{\tilde{\alpha}_2} (\delta_{\tilde{\alpha}_1\tilde{\alpha}_2} - \eta k_{\tilde{\alpha}_1\tilde{\alpha}_2}) \epsilon_{i;\tilde{\alpha}_2} (t)\]
This is a repeated multiplication by a constant matrix:
\[U_{\tilde{\alpha}_1\tilde{\alpha}_0} (t) = [(\delta - \eta k)^t]_{\tilde{\alpha}_1\tilde{\alpha}_0} = \sum_{\tilde{\alpha}_1,...,\tilde{\alpha}_{t-1}} (\delta_{\tilde{\alpha}_t\tilde{\alpha}_{t-1}} - \eta k_{\tilde{\alpha}_t\tilde{\alpha}_{t-1}}) \cdots (\delta_{\tilde{\alpha}_1\tilde{\alpha}_0} - \eta k_{\tilde{\alpha}_1\tilde{\alpha}_0}).\]
The solution is given by
\[\epsilon_{i;\tilde{\alpha}_1} (t) = \sum_{\tilde{\alpha}_2} U_{\tilde{\alpha}_1\tilde{\alpha}_2} (t) \epsilon_{i;\tilde{\alpha}_2} (0),\]
and ( U(t) \to 0 ) as ( t \to \infty ) so that the error vanishes: ( z_{i;\tilde{\alpha}} \to y_{i;\tilde{\alpha}} ).
We still have to solve the difference equation for the test error:
\[Z_{i;\delta}(t + 1) = Z_{i;\delta}(t) - \eta \sum_{\tilde{\alpha}} k_{\delta \tilde{\alpha}} \epsilon_{i;\tilde{\alpha}}(t)\]
but we are interested in what happens at the end (time ( t )).
\[Z_{i;\delta}(t) = Z_{i;\delta}(0) - \sum_{\tilde{\alpha} \in A} k_{\delta \tilde{\alpha}} \left( \eta \sum_{s=0}^{t-1} \epsilon_{i;\tilde{\alpha}}(s) \right)\]
Now, let’s investigate what happens if ( t \to \infty ).
\[\begin{aligned}
Z_{i;\delta}(\infty) &= Z_{i;\delta}(0) - \sum_{\tilde{\alpha} \in A} k_{\delta \tilde{\alpha}} \left\{ \sum_{s=0}^{\infty} \eta \epsilon_{i;\tilde{\alpha}}(s) \right\} \\
&= Z_{i;\delta}(0) - \sum_{\tilde{\alpha} \in A} k_{\delta \tilde{\alpha}} \left\{ \sum_{s=0}^{\infty} \eta \sum_{\tilde{\alpha}_1} U_{\tilde{\alpha} \tilde{\alpha}_1} (s) \epsilon_{i;\tilde{\alpha}_1}(0) \right\} \\
&= Z_{i;\delta}(0) - \sum_{\tilde{\alpha}, \tilde{\alpha}_1 \in A} k_{\delta \tilde{\alpha}} \left\{ \eta \sum_{s=0}^{\infty} \left[ (\delta - \eta k)^s \right]_{\tilde{\alpha} \tilde{\alpha}_1} \right\} \epsilon_{i;\tilde{\alpha}_1}(0) \\
&= Z_{i;\delta}(0) - \sum_{\tilde{\alpha}, \tilde{\alpha}_1 \in A} k_{\delta \tilde{\alpha}} \left\{ \eta \left[ \delta - (\delta - \eta k) \right]^{-1} \right\}_{\tilde{\alpha} \tilde{\alpha}_1} \epsilon_{i;\tilde{\alpha}_1}(0) \\
&= Z_{i;\delta}(0) - \sum_{\tilde{\alpha}, \tilde{\alpha}_1 \in A} k_{\delta \tilde{\alpha}} \tilde{k}_{\tilde{\alpha}_1} \epsilon_{i;\tilde{\alpha}_1}(0)
\end{aligned}\]
Compare gradient descent vs. the direct optimization solution:
\[\begin{aligned}
z_{i;\delta}(\infty) &= Z_{i;\delta}(0) - \sum_{\tilde{\alpha}, \tilde{\alpha}_1 \in \mathcal{A}} k_{\delta \tilde{\alpha}} \tilde{k}^{\tilde{\alpha} \tilde{\alpha}_1} \epsilon_{i;\tilde{\alpha}_1}(0) \\
z_{i}(x_{\delta}; \theta^*) &= \sum_{\tilde{\alpha}, \tilde{\alpha}_1 \in A} k_{\delta \tilde{\alpha}_1} \tilde{k}^{\tilde{\alpha} \tilde{\alpha}_1} y_{i;\tilde{\alpha}_1}.
\end{aligned}\]
- Those are same if ( Z_{i;\delta}(0) = 0 ), e.g. if ( W_{ij}(0) = 0 ).
- Otherwise, linear models have algorithm independence (different ( \eta ) yields different predictions).
- Importantly, ( k_{\delta \tilde{\alpha}_1} ) is fixed, and the ( \phi_i(x) ) do not evolve.
7. Quadratic Model Dynamics
The weights will update as
\[\begin{aligned}
W_{ij}(t + 1) &= W_{ij}(t) - \eta \left. \frac{\partial \mathcal{L}_A}{\partial W_{ij}} \right|_{W_{ij}=W_{ij}(t)} \\
&= W_{ij}(t) - \eta \sum_{\tilde{\alpha}} \phi^{E}_{ij;\tilde{\alpha}} (t) \epsilon_{i;\tilde{\alpha}}(t).
\end{aligned}\]
While the model and effective features update as
\[\begin{aligned}
Z_{i;\delta}(t + 1) &= Z_{i;\delta}(t) + \sum_{j} dW_{ij}(t) \phi^{E}_{ij;\delta}(t) + \frac{\epsilon}{2} \sum_{j_1,j_2} dW_{ij_1}(t) dW_{ij_2}(t) \psi_{j_1j_2}(x_{\delta}), \\
\phi^{E}_{ij;\delta}(t + 1) &= \phi^{E}_{ij;\delta}(t) + \epsilon \sum_{k=0}^{n_f} dW_{ik}(t) \psi_{kj}(x_{\delta}).
\end{aligned}\]
8. Model prediction dynamics
The weights will update as
\[\begin{aligned}
Z_{i;\delta}(t + 1) &= Z_{i;\delta}(t) + \sum_{j} dW_{ij}(t) \phi^{E}_{ij;\delta}(t) + \frac{\epsilon}{2} \sum_{j_1,j_2} dW_{ij_1}(t) dW_{ij_2}(t) \psi_{j_1j_2}(x_{\delta}), \\
&= Z_{i;\delta}(t) + \sum_{j} \left[ -\eta \sum_{\tilde{\alpha}} \phi^{E}_{ij;\tilde{\alpha}}(t) \epsilon_{i;\tilde{\alpha}}(t) \right] \phi^{E}_{ij;\delta}(t) \\
&\quad + \frac{\epsilon}{2} \sum_{j_1,j_2=0}^{n_f} \left[ -\eta \sum_{\tilde{\alpha}_1} \phi^{E}_{ij_1;\tilde{\alpha}_1}(t) \epsilon_{i;\tilde{\alpha}_1}(t) \right] \left[ -\eta \sum_{\tilde{\alpha}_2} \phi^{E}_{ij_2;\tilde{\alpha}_2}(t) \epsilon_{i;\tilde{\alpha}_2}(t) \right] \psi_{j_1j_2}(x_{\delta}), \\
&= Z_{i;\delta}(t) - \eta \sum_{\tilde{\alpha}} \textcolor{red}{\sum_{j} \phi^{E}_{ij;\delta}(t) \phi^{E}_{ij;\tilde{\alpha}}(t)} \epsilon_{i;\tilde{\alpha}}(t) \\
&\quad + \frac{\eta^2}{2} \sum_{\tilde{\alpha}_1,\tilde{\alpha}_2} \textcolor{red}{ \sum_{j_1,j_2} \epsilon \psi_{j_1j_2}(x_{\delta}) \phi^{E}_{ij_1;\tilde{\alpha}_1}(t) \phi^{E}_{ij_2;\tilde{\alpha}_2}(t)} \epsilon_{i;\tilde{\alpha}_1}(t) \epsilon_{i;\tilde{\alpha}_2}(t)
\end{aligned}\]
To better understand this from the dual sample-space picture, let’s analogously define an effective kernel
\[k^{E}_{ij;\delta_1\delta_2} (\theta) = \sum_{j=0}^{n_f} \phi^{E}_{ij}(x_{\delta_1}; \theta) \phi^{E}_{ij}(x_{\delta_2}; \theta),\]
which measures a parameter-dependent similarity between two inputs ( x_{\delta_1} ) and ( x_{\delta_2} ) using our effective features ( \phi^{E}{ij}(x{\delta}; \theta) ).
This last line suggests that an important object worth defining is the meta kernel
\(\mu_{\delta_0\delta_1\delta_2} \equiv \sum_{j_1,j_2=0}^{n_f} \epsilon \psi_{j_1j_2}(x_{\delta_0}) \phi_{j_1}(x_{\delta_1}) \phi_{j_2}(x_{\delta_2})\)
\(= \sum_{j_1,j_2=0}^{n_f} \epsilon \psi_{j_1j_2}(x_{\delta_0}) \phi^{E}_{j_1i_1}(x_{\delta_1}; \theta) \phi^{E}_{j_2i_2}(x_{\delta_2}; \theta) + O(\epsilon^2),\)
- This is a parameter-independent tensor given entirely in terms of the fixed ( \phi_j(x) ) and ( \psi_{j_1j_2}(x) ) that define the model.
- For a fixed input ( x_{\delta_0} ), ( \mu_{\delta_0\delta_1\delta_2} ) computes a different feature-space inner product between the two inputs, ( x_{\delta_1} ) and ( x_{\delta_2} ).
- Due to the inclusion of ( \epsilon ) into the definition of ( \mu_{\delta_0\delta_1\delta_2} ), we should think of it as being parametrically small too.
Using the definition of ( k^{E}{ij;\delta_1\delta_2} (\theta) ) and ( \mu{\delta_0\delta_1\delta_2} ), we have the following.
\[\begin{aligned}
Z_{i;\delta}(t + 1) &= Z_{i;\delta}(t) - \eta \sum_{\tilde{\alpha}} \left[ \sum_{j} \phi^{E}_{ij;\delta}(t) \phi^{E}_{ij;\tilde{\alpha}}(t) \right] \epsilon_{i;\tilde{\alpha}}(t) \\
&\quad + \frac{\eta^2}{2} \sum_{\tilde{\alpha}_1,\tilde{\alpha}_2} \left[ \epsilon \sum_{j_1,j_2} \phi^{E}_{ij_1;\tilde{\alpha}_1}(t) \phi^{E}_{ij_2;\tilde{\alpha}_2}(t) \psi_{j_1j_2}(x_{\delta}) \right] \epsilon_{i;\tilde{\alpha}_1}(t) \epsilon_{i;\tilde{\alpha}_2}(t) \\
&= Z_{i;\delta}(t) - \eta \sum_{\tilde{\alpha}} k^{E}_{ii;\delta\tilde{\alpha}}(t) \epsilon_{i;\tilde{\alpha}}(t) + \frac{\eta^2}{2} \sum_{\tilde{\alpha}_1,\tilde{\alpha}_2} \mu_{\delta\tilde{\alpha}_1\tilde{\alpha}_2} \epsilon_{i;\tilde{\alpha}_1}(t) \epsilon_{i;\tilde{\alpha}_2}(t) + O(\epsilon^2)
\end{aligned}\]
This is a coupled nonlinear difference equation…
Now, to solve the coupled nonlinear difference equation, we compute effective kernel dynamics
\[\begin{aligned}
\phi^{E}_{ij;\delta}(t + 1) &= \phi^{E}_{ij;\delta}(t) + \epsilon \sum_{k=0}^{n_f} dW_{ik}(t) \psi_{kj}(x_{\delta}) \\
&= \phi^{E}_{ij;\delta}(t) + \epsilon \sum_{k=0}^{n_f} \left[ -\eta \sum_{\tilde{\alpha}} \phi^{E}_{ik;\tilde{\alpha}}(t) \epsilon_{i;\tilde{\alpha}}(t) \right] \psi_{kj}(x_{\delta}) \\
&= \phi^{E}_{ij;\delta}(t) - \eta \sum_{\tilde{\alpha}} \left[ \epsilon \sum_{k=0}^{n_f} \psi_{kj}(x_{\delta}) \phi^{E}_{ik;\tilde{\alpha}}(t) \right] \epsilon_{i;\tilde{\alpha}}(t)
\end{aligned}\]
To compute the dynamic of effective kernel,
\[\begin{aligned}
\sum_{j} \phi^{E}_{ij;\delta_1}(t + 1) \phi^{E}_{ij;\delta_2}(t + 1) &= \sum_{j} \phi^{E}_{ij;\delta_1}(t) \phi^{E}_{ij;\delta_2}(t) \\
&\quad - \eta \sum_{\tilde{\alpha}} \left[ \sum_{j,k} \epsilon \psi_{kj}(x_{\delta_1}) \phi^{E}_{ij;\delta_2}(t) \phi^{E}_{ik;\tilde{\alpha}}(t) \right] \epsilon_{i;\tilde{\alpha}}(t) \\
&\quad - \eta \sum_{\tilde{\alpha}} \left[ \sum_{j,k} \epsilon \psi_{kj}(x_{\delta_2}) \phi^{E}_{ij;\delta_1}(t) \phi^{E}_{ik;\tilde{\alpha}}(t) \right] \epsilon_{i;\tilde{\alpha}}(t) + O(\epsilon^2)
\end{aligned}\]
Above equation could be rearranged as follows.
\[\begin{aligned}
k^{E}_{ii;\delta_1\delta_2}(t + 1) &= k^{E}_{ii;\delta_1\delta_2}(t) - \eta \sum_{\tilde{\alpha}} (\mu_{\delta_1\tilde{\alpha}} + \mu_{\delta_2\tilde{\alpha}}) \epsilon_{i;\tilde{\alpha}}(t) + O(\epsilon^2)
\end{aligned}\]
Linear difference equation, with ( \mu_{\delta_1\delta_2\tilde{\alpha}} ) playing the role of ( k_{\delta\tilde{\alpha}} \dots )
The model predictions will update as
\[\begin{aligned}
Z_{i;\delta}(t + 1) &= Z_{i;\delta}(t) - \eta \sum_{\tilde{\alpha}} k^{E}_{ii;\delta\tilde{\alpha}}(t) \epsilon_{i;\tilde{\alpha}}(t) \\
&\quad + \frac{\eta^2}{2} \sum_{\tilde{\alpha}_1,\tilde{\alpha}_2} \mu_{\delta\tilde{\alpha}_1\tilde{\alpha}_2} \epsilon_{i;\tilde{\alpha}_1}(t) \epsilon_{i;\tilde{\alpha}_2}(t) + O(\epsilon^2)
\end{aligned}\]
While the effective kernel will update as
\[\begin{aligned}
k^{E}_{ii;\delta_1\delta_2}(t + 1) &= k^{E}_{ii;\delta_1\delta_2}(t) - \eta \sum_{\tilde{\alpha}} (\mu_{\delta_1\tilde{\alpha}} + \mu_{\delta_2\tilde{\alpha}}) \epsilon_{i;\tilde{\alpha}}(t) + O(\epsilon^2)
\end{aligned}\]
- These joint updates are coupled difference equations, and the first is nonlinear in the training error.
- We are now going to solve these equations in a closed form to leading order in ( \epsilon ) using perturbation theory.